Bilangan Pecahan

Banyak yang mengira bahwa bilangan pecahan adalah bilangan yang berbentuk a/b dengan a sebagai pembilang dan b sebagai penyebut. Jika begitu, apakah 6/2 termasuk bilangan pecahan?

Tokoh Bilangan Pecahan

Sejarah bilangan pecahan memang dimulai sejak zaman Mesir kuno. Tetapi cara penulisannya masih belum seperti sekarang ini, masih menggunakan simbol-simbol gambar.

Al-Qalasadi, seorang intelektual Andalusia, adalah matematikawan pertama yang memperkenalkan simbol garis horizontal di antara pembilang dan penyebut pada bilangan pecahan. Selain itu, beliau juga mencetuskan simbol-simbol aljabar lainnya, seperti simbol penjumlahan, pengurangan, perkalian, pembagian, akar, dan lain-lain.

Al-Qalasadi terlahir dengan nama lengkap Abu Al-Hasan bin Ali bin Muhammad Al-Qalasadi. Pada mulanya Al-Qalasadi hanya menekuni ilmu faraid (ilmu tentang pembagian hak waris).

Berangkat dari ilmu faraid yang dikenal banyak menggunakan penghitungan bilangan pecahan, akhirnya beliau menjadi matematikawan hebat. Selain itu, Al-Qalasadi juga dikenal sebagai ahli hukum (fiqih).

Sedangkan penulisan bilangan pecahan dalam bentuk desimal, pertama kali diperkenalkan oleh Al-Kasyi atau Al-Qasyani. Penulisan berikut cara penghitungannya diabadikan dalam bukunya yang berjudul Miftah Al-Hisab atau Kunci Perhitungan.

Al-Kasyi terlahir dengan nama lengkap Ghiyatuddin Jamsydin bin Mahmud bin Muhammad al-Kasyi. Selain seorang matematikawan, beliau juga seorang astronom yang tersohor.

Pengertian Bilangan Pecahan

Bilangan pecahan adalah bilangan yang nilainya kurang atau lebih dari bilangan bulat. Bilangan pecahan nilainya tidak utuh, tidak seperti bilangan bulat.

Bentuk umum bilangan pecahan adalah

Dengan a dan b adalah bilangan bulat, b ≠ 0, serta b bukan faktor dari a.

Bilangan pecahan tidak hanya dilambangkan dalam bentuk a/b. Bilangan pecahan juga bisa dilambangkan dalam bentuk desimal, persen (%), atau permil (‰).

Jika kita makan kue dan sisanya tinggal separuh maka sisa separuh tersebut dapat dinyatakan dengan bilangan pecahan 1/2, 0,5, atau 50%.

Jenis Bilangan Pecahan

Berdasarkan perbandingan antara pembilang dan penyebutnya, bilangan pecahan dibagi menjadi dua, yaitu pecahan sejati dan pecahan tidak sejati.

Bilangan Pecahan Sejati (Pecahan Murni)

Bilangan pecahan sejati adalah bilangan pecahan yang nilainya antara 0 sampai 1 atau antara −1 sampai 0.

Jika diibaratkan sepotong kue yang dibagi-bagi maka setiap bagian kue tersebut merupakan pecahan sejati karena nilainya kurang dari 1.

Ciri bilangan pecahan sejati
Jika a sebagai pembilang dan b sebagai penyebut serta b ≠ 0 maka ciri pecahan sejati adalah

|a| < |b| 

Contoh bilangan pecahan sejati

Bilangan Pecahan Tidak Sejati (Pecahan Campuran) 

Bilangan pecahan tidak sejati adalah bilangan pecahan yang nilainya lebih dari 1 atau kurang dari −1.

Jika 3 meter kain dipotong menjadi dua bagian sama panjang maka setiap potongan panjangnya 3/2 meter atau 1½ meter. 

Berdasarkan ilustrasi di atas, bilangan pecahan tidak sejati dapat ditulis dalam bentuk pecahan tunggal dan pecahan campuran.

• Pecahan tunggal : 3/2 


• Pecahan campuran : 1½

Oleh karena itu, bilangan pecahan tidak sejati sering disebut dengan bilangan pecahan campuran, yaitu bilangan pecahan yang tersusun dari bilangan bulat dan bilangan pecahan sejati.

Ciri bilangan pecahan tidak sejati
Jika a adalah pembilang dan b adalah penyebut serta b ≠ 0 maka ciri bilangan pecahan tidak sejati adalah

|a| > |b|

dengan syarat b bukan faktor dari a atau a tidak habis dibagi b.

Contoh bilangan pecahan tidak sejati

12/3 bukan termasuk bilangan pecahan tidak sejati karena 3 adalah faktor dari 12 atau karena 12 habis dibagi 3.

Berdasarkan penyebutnya, bilangan pecahan dapat dibagi menjadi 3 jenis, yaitu bilangan pecahan senama, pecahan desimal, persen dan permil.

Bilangan Pecahan Senama

Pecahan senama adalah pecahan yang mempunyai penyebut yang sama.

Pecahan Desimal

Pecahan desimal adalah pecahan yang penyebutnya 10ⁿ (10, 100, 1000, …) dengan n adalah bilangan asli. Penulisannya ditandai dengan tanda koma (,).

Banyaknya angka di belakang koma menunjukkan nilai n. Jika ada 2 angka di belakang koma maka pembaginya adalah 10² atau 100.

Persen

Pecahan dalam bentuk persen adalah pecahan yang dengan pembagi 100. Notasinya dilambangkan dengan simbol %.

8/100   = 8%
42/100 = 42%
60/100 = 60%

Permil

Pecahan permil adalah pecahan dengan pembagi 1000. Notasinya dilambangkan ‰.

7/1000   = 7‰
50/1000 = 50‰

Bilangan Rasional

Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk a/b dengan a dan b adalah bilangan bulat serta b ≠ 0.

Definisi di atas sering disalahfahami sebagai definisi bilangan pecahan.

Perhatikan contoh berikut ini!

• 2 dapat dinyatakan dalam bentuk 2/1, 8/4, atau 100/50 sehingga 2 dapat dikatakan sebagai bilangan rasional.


• 0,25 dapat dinyatakan dalam bentuk 1/4 atau 25/100 sehingga 0,25 termasuk bilangan rasional.

Dari contoh di atas dapat disimpulkan bahwa bilangan rasional meliputi bilangan bulat dan bilangan pecahan.

Jadi, semua bilangan pecahan adalah bilangan rasional, tetapi tidak semua bilangan rasional adalah pecahan.

6/2 adalah bilangan rasional tetapi bukan bilangan pecahan karena 6/2 adalah 3.

Bagaimana dengan bilangan yang tidak dapat dinyatakan dalam bentuk a/b ? Bilangan itu disebut bilangan irrasional.

Beberapa bentuk akar, trigonometri, dan logaritma merupakan contoh bilangan rasional.

√3 = 1,73205…
e   = 2,71828…
π   = 3,14159…

Nilai π yang sering diwakili 22/7 sebenarnya hanya pendekatan.

π      = 3,14159…
22/7 = 3.14285…

Bilangan Pecahan Senilai (Ekuivalen)

Untuk memahami pecahan senilai perhatikan ilustrasi berikut ini!

Pada gambar (1), persegi tersebut terbagi menjadi 2 bagian berarti daerah yang diarsir adalah 1/2 bagian.
Pada gambar (2), persegi tersebut terbagi menjadi 4 bagian berarti daerah yang diarsir adalah 2/4 bagian.
Pada gambar (1), persegi tersebut terbagi menjadi 4 bagian berarti daerah yang diarsir adalah 4/8 bagian.

Dari gambar tersebut terlihat bahwa daerah yang diarsir pada ketiga persegi tersebut mempunyai luas yang sama sehingga

Pecahan-pecahan yang mempunyai nilai yang sama inilah yang disebut pecahan senilai atau ekuivalen.

Ciri pecahan senilai
Untuk a, b, c, dan d bilangan bulat serta b ≠ 0, d ≠ 0 berlaku

Contoh:

Membanding Bilangan Pecahan Tidak Senilai

Bilangan pecahan yang tidak senilai adalah bilangan pecahan yang mempunyai nilai lebih besar atau lebih kecil dari bilangan pecahan yang lain.

Membandingkan Bilangan Pecahan yang Penyebutnya Sama

Jika dua bilangan pecahan mempunyai penyebut yang sama besar maka pecahan dengan pembilang yang lebih besar mempunyai nilai lebih besar.

Membandingkan Bilangan Pecahan yang Pembilangnya Sama

Jika dua pecahan mempunyai pembilang yang sama besar maka pecahan dengan penyebut lebih besar mempunyai nilai lebih kecil.

Membanding Bilangan Pecahan yang Mempunyai Pembilang dan Penyebut Berbeda

Untuk a, b, c, dan d bilangan bulat serta b ≠ 0, d ≠ 0 berlaku

Contoh:
Manakah yang lebih besar dari dua pecahan berikut?

Kita periksa dengan perkalian berikut ini.

2 × 5 < 4 × 3
    10 < 12

Sehingga   

Penjumlah dan Pengurangan Bilangan Pecahan

Penjumlahan dan Pengurangan Bilangan Pecahan Senama

Menjumlahkan dan mengurangkan bilangan pecahan senama (penyebutnya sama) dapat dilakukan dengan menjumlahkan dan mengurangkan pembilangnya.

Penjumlahan dan Pengurangan Bilangan Pecahan yang tidak Senama

Perhatikan ilustrasi berikut ini!

Untuk menjumlahkan dan mengurangkan kedua pecahan tersebut kita gunakan pecahan yang senilai (ekuivalen) dari kedua pecahan tersebut.

Berikut ini ilustrasinya.

Jadi,

Dengan demikian. Untuk menjumlahkan dan mengurangkan bilangan pecahan yang tidak senama dilakukan dengan cara menyamakan penyebutnya.

Cara lain untuk melakukan operasi tersebut adalah dengan melakukan perkalian silang.

Penjumlahan dan Pengurangan Bilangan Pecahan Campuran

Menjumlahkan atau mengurangkan dua bilangan campuran dengan cara menjumlahkan atau mengurangkan bagian bilangan bulat dilanjutkan dengan bagian bilangan pecahan.

Sifat Penjumlahan dan Pengurangan Bilangan Pecahan

Tidak Bersifat Tertutup

Hasil dari penjumlahan dan pengurangan bilangan pecahan tidak selalu menghasilkan bilangan pecahan.

Sifat Komutatif

Penjumlahan bilangan pecahan bersifat komutatif (pertukaran).

Pengurangan bilangan pecahan tidak bersifat komutatif.

Sifat Asosiatif

Penjumlahan dan pengurangan bilangan pecahan bersifat asosiatif (pengelompokan).

Perkalian dan Pembagian Bilangan Pecahan

Perkalian Bilangan Pecahan

Perhatikan ilustrasi berikut!

Hasil perkalian 2/3 × 1/5 adalah daerah yang berwarna abu-abu. Pada daerah tersebut terdapat 2 kotak di antara 15 kotak atau 2/15 bagian.

Jadi,

Dengan demikian, mengalikan bilangan pecahan dapat dilakukan dengan mengalikan masing-masing pembilang dan penyebutnya.

Sedangkan untuk mengalikan bilangan pecahan campuran dilakukan setelah mengubah keduanya menjadi pecahan tunggal.

Pembagian Bilangan Pecahan

Perhatikan ilustrasi berikut ini!

Berdasarkan ilustrasi di atas terlihat bahwa air 1/2 gelas dibagi menjadi 2 bagian yang masing-masing berisi 1/4 gelas. Dapat dituliskan

Dengan demikian, membagi bilangan pecahan dapat dilakukan dengan cara mengalikan silang antara pembilang dan penyebutnya.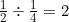

Membagi pecahan a dengan pecahan b juga berarti mengalikan pecahan a dengan kebalikan pecahan b.

Contoh:

Sifat Perkalian dan Pembagian Bilangan Pecahan

Tidak bersifat Tertutup

Hasil dari perkalian dan pembagian bilangan pecahan tidak selalu menghasilkan bilangan pecahan.

Sifat Komutatif

Perkalian bilangan pecahan bersifat komutatif (pertukaran)

Pembagian bilangan pecahan tidak bersifat komutatif.

Sifat Asosiatif

Perkalian dan pembagian bilangan pecahan bersifat asosiatif (pengelompokan)

Silakan dilanjutkan ke materi berikutnya, Pola Bilangan.

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.